yaohaoyou

T1

原题：$\color{#ffffff}\text{CF1399E2 Weights Division (hard version) }$

$\color{#ffffff}\text{CF 2200}$

题意

给你一棵以 $1$ 为根的香蕉树，每条边有边权 $w_i$ 和花费 $c_i$。

每个叶子节点都有一只 liangbowen，他们都想去 $1$ 节点吃香蕉。

但是 liangbowen 们急着去杀戮，所以需要保证 $\sum_\text{u is liangbowen}w(1,u)\le lim$，$\text{u is liangbowen}$ 当且仅当 $u$ 是叶子节点，$w(x,y)$ 表示 $x$ 到 $y$ 的树上距离。

lubenwei 可以开挂，将 $w_i \gets \lfloor\dfrac{w_i}{2}\rfloor$，吸引网管 $c_i$ 点注意。

lubenwei 不希望开挂太多导致被网管封号，所以请最小化网管的注意使得 liangbowen 们可以准时杀戮，保证有解。

$n\le 10^5,c_i\in \{1,2\},1\le w_i\le 10^6,1\le lim \le10^{16}$。

$\tiny\text{形式化题意：}$

给出一个结点数量为 $n$ 的边带权的有根树，树的根结点为 $1$。你可以进行以下操作。

选定任意一条权值为 $w_i$ 的边，使 $w_i \gets \lfloor \frac{w_i}{2} \rfloor$，花费为 $c_i$ 且 $c_i \in \{1, 2\}$。

你需要回答最小的花费，使得 $\sum\limits_{v\in leaves}w(1,v)\leq S$。

Easy Version：$c_i=1$。

题解

先考虑 Easy Version，由于保证 $c_i=1$，所以直接贪心即可。

首先可以用树形 DP 求出删掉当前边的贡献，设 $dp_i$ 表示 $i$ 的子树中有多少个叶子节点，不难得出
$dp_u = \begin{cases}\sum dp_{son} & u \ne leaf \\ 1 & u=leaf \end{cases}$。

设一条边的贡献为 $s_i$，儿子为 $v$，则 $s_i=dp_v \times (w_i-\lfloor \frac{w_i}{2} \rfloor)$。将 $s_i$ 丢进大根堆，每次取出 $s_i$ 最大的边模拟进行操作即可。

再回到 Hard Version。

错的做法

此时还想贪心就变得非常困难，所以可以思考将答案划分成选择边权花费为 $1$ 的答案 $+$ 选择边权花费为 $2$ 的答案。当只选择边权花费为 $1$ 的答案时，可以确定操作的顺序（即 Easy Version），同理，只选择边权花费为 $2$ 的答案也可以提前处理操作顺序。

然后只要枚举要操作花费为 $1$ 的次数，并计算花费为 $2$ 的次数即可。此时的时间复杂度为 $O(n^2\times \log_2 n)$，无法通过此题。

观察性质，发现操作花费为 $1$ 的次数越多，操作花费为 $2$ 的次数就越少。所以可以将计算花费为 $2$ 的次数用双指针优化掉，时间复杂度为 $O(n \times \log_2 n)$，记得处理操作全是花费为 $1$ 和 $2$ 的答案。

$\color{white}code$

T2

原题：$\color{#ffffff}\text{CF1059E Split the Tree}$

$\color{#ffffff}\text{CF 2400}$

题意

lbw 和 Mathew 正在宿舍打 21 点，但是他把牌摆成了一棵树的形状。

规则就是在树上找一条深度依次递增的链，使得链上扑克牌的点数和 $\le 21$。同时还有一种规则叫做五龙，就是当你取得 $5$ 张牌时，游戏就结束了。

但是 lbw 想要练习出千，于是把 21 点变成 $L$ 点，把 $5$ 龙变成 $S$ 龙，把扑克牌点数的集合变成自然数集。

lbw 有透视眼，可以提前看到每个节点的牌的点。lbw 用最短的时间秒杀 Mathew，所以希望总局数最少。

请求 lbw 最少选出多少条链可以使得每张牌刚好被拿走一次，且牌数 $\le L$，点数和 $\le S$，需要判无解。

$n\le 10^5,L\le10^5,S\le 10^{18}$。

$\tiny\text{形式化题意：}$

给一棵带点权的树，每次选一条深度依次递增的链，链长 $\le L$，链上点权和 $\le S$。想让每个点当且仅当被覆盖一次，求链数最小值，需要判无解。

题解

显然，当有一个点的点权 $>S$ 时就无解，否则有解。

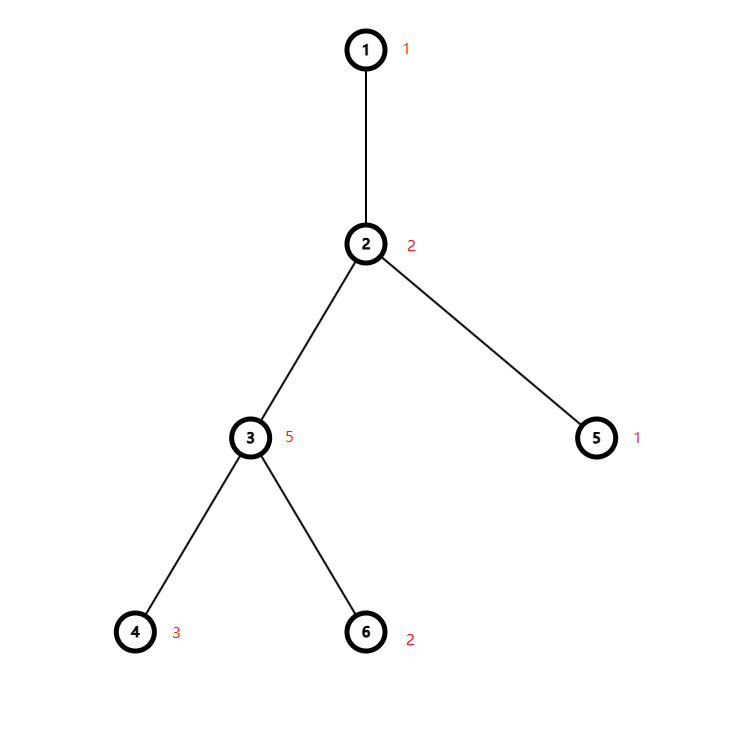
考虑一个贪心结论，对于 $u$ 和 $u$ 的儿子 $v$，显然从 $u$ 往上能到达的点会比 $v$ 往上到达的点更高或相同，所以节点 $u$ 一定会选择剩余步数最多的儿子节点进行转移。

可以先使用树上倍增求出每个节点 $u$ 能到达的最高祖先，计 $up_u$ 表示从 $u$ 节点最多再往上跳 $up_u$ 步。

考虑树形DP。

设 $f_u$ 表示将 $u$ 的子树覆盖完的链的最少条数，$g_u$ 表示 $u$ 的子树内剩余的最大步数。

$g_u=\max_\text{v is son of u}(g_v-1) \\ f_u=\sum_\text{v is son of u}f_v$

若此时 $g_u=0$，说明无法从子树内已有的链往上延申，所以需要开一条新链，即 $f_u++,g_u=up_u$。

否则不需要进行修改。

钦定树的根为 $1$，则答案为 $f_1$。

$\color{white}code$